Mandelbrot Set

Prerequisite Knowledge link

Mandelbrot Set is a famous fractal. It is generated by a recursive function $z_{n+1}=z_n^2+z_0$. Given a value of $z_0$, $z_0$ is in the Mandelbrot Set if and only if $z_n$ does not go to infinity as $n$ increases.

Make Mandelbrot Set in Grapycal link

This tutorial goes with the example file “mandelbrot.grapycal”. To open the file, you need grapycal_torch extension installed.

Initialize link

First, we generate a complex plane and store it into both variable z0 and z. The complex plane include all complex numbers in a certain range (with limited resolution), so we can iterate them all together.

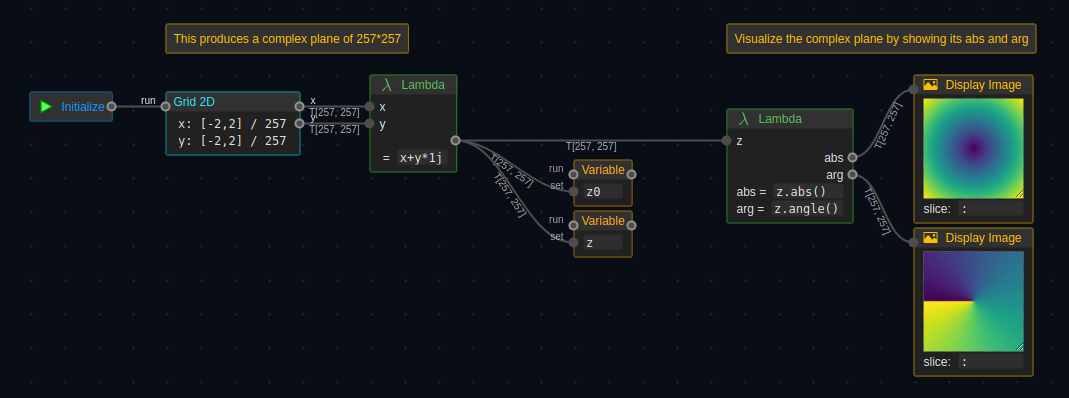
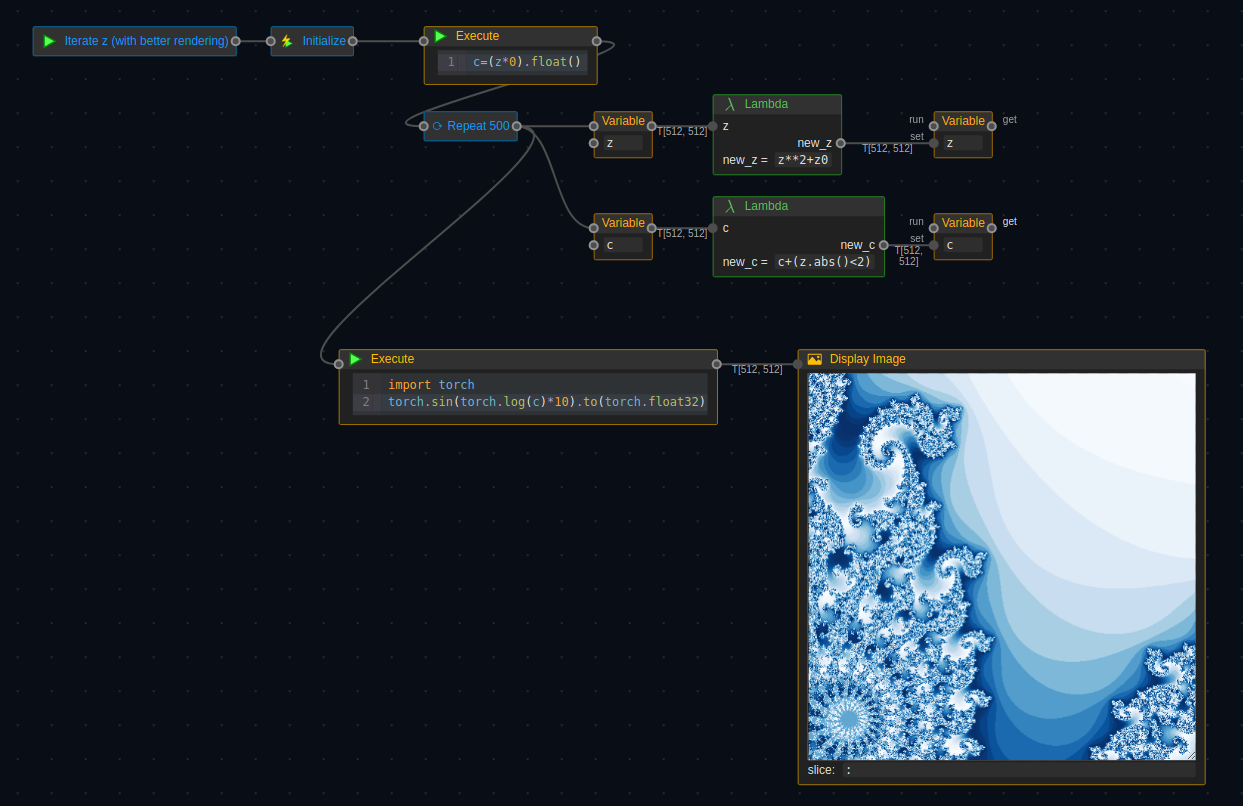
Iterate z link

The program repeats 50 times: take z, calculate the new z, store the value back to z.

The outcome is a plain image of Mandelbrot Set.

Iterate z (With Better Rendering) link

To make it prettier, we introduce a variable c to record the time abs(z) exceeds 2.

What’s Next? link

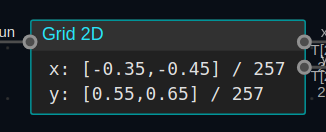
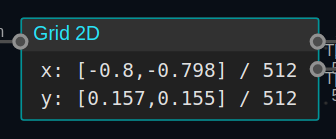
Zoom in to the details of Mandelbrot Set by adjusting the GridNode’s parameters.

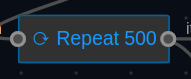
Tip: Iterate more than 50 times to get finer result.

These are some examples:

Try other rendering techniques for Mandelbrot Set. A good technique is that instead of render from $c$, render from $sin(log(c)*10)$. The $sin$ make the color map periodic. The $log$ make the color map distribute evenly w.r.t scaling.

Make other kinds of fractals such as Julia Set. See https://en.wikipedia.org/wiki/Mandelbrot_set#See_also.